Flow Loss Coefficient - Rectangular Pipe

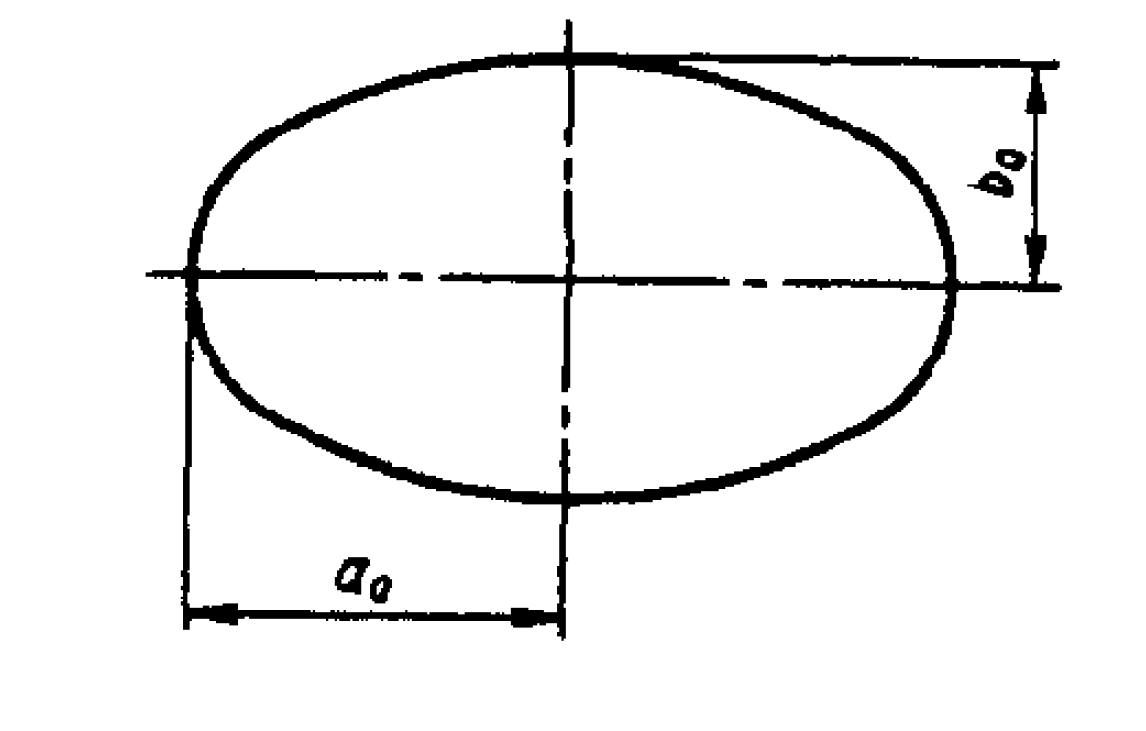
$ a_0$ - semi-major axis
$ b_0$ - semi-minor axis

Elliptical channels are found in culverts, sewer systems, and biomedical applications like artificial vessels. Their non-circular shape enables better flow under partial-fill conditions while maintaining compact profiles.

Here you’ll find pressure loss coefficients (K-factors) specific to elliptical cross-sections, along with guidance on computing equivalent hydraulic diameter for accurate head loss analysis. While round pipes dominate datasets, elliptical flows are critical in certain engineered systems.

For pipes of rectangular cross section, the flow loss coefficient is defined as:

$$ \lambda = \frac{\Delta p}{(\rho w_0^2 /2)(\ell/D_0)} = k_\mathrm{ell}\lambda_\mathrm{round}$$

where $ \lambda_\mathrm{round}$ is the flow loss coefficient of an equivalent channel of round cross section. See associated calculators for a round channel that is smooth, has uniform sand grain roughness, or has non-uniform roughness.

An equivalent hydraulic diameter for an elliptical channel:

$$ \mathrm{D}_H = \frac{4A}{P} \approx \frac{\pi a_0 b_0}{0.983a_0 + 0.311b_0 + 0.287b_0^2/a_0} $$

where $ A $ is cross sectional area, and $ P $ is the perimeter

Reynolds number is based on the hydraulic diameter:

$$ \mathrm{Re} = \frac{V \mathrm{D}_H}{\nu}$$

For laminar flow regime ($ \mathrm{Re} \lt 2000 $):

$$ k_{ell} = \frac{1}{8} \left( \frac{\mathrm{D}_H}{b_0} \right)^2 \left[ 1 + \left( \frac{b_0}{a_0}\right)^2 \right] $$

For turbulent flow regime ($ \mathrm{Re} \gt 2000 $), $ k_{ell} \approx 1 $